【はじめに】
2007年にLustig氏が“Sparse MRI”を発表してから約10年経ち、現在では多くのメーカーが圧縮センシングをMRIの画像再構成に応用した技術をリリースしています。最近では一般演題の発表でも圧縮センシングをMRIに応用し臨床上の有用性を評価する内容を散見するようになってきました。
しかし、信号収集の概念はこれまでの診療放射線技師にとって常識であったナイキスト理論に基づくものではないため、多くの人が慣れない感覚をもっているのではないかと思います。実際、私自身も“スパース”、“L1ノルム”、“最適化数学”など全く聞いたことがない言葉ばかりで、数式を見るだけでも辛かった記憶があります。
この記事ではLustig氏の“Sparse MRI”で苦しみながら学んで理解したことを表現したいと思います。
【圧縮センシングMRIの発想】
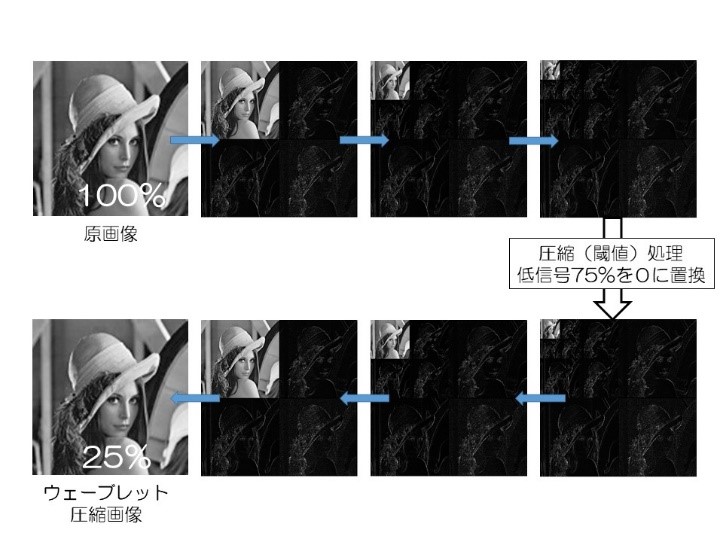
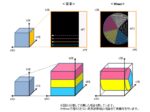
まずはウェーブレット圧縮をご存知でしょうか?ウェーブレット圧縮はJPEG2000等で用いられる画像圧縮方法です。
ここで、青矢印はウェーブレット変換(逆変換)といいます。また、ウェーブレット変換によって得られた画像をウェーブレット画像(スパース画像)といいます。そしてスパース・疎とは大部分の要素が0ばかりであることを示します。ウェーブレット画像は、信号が僅かな黒いピクセルばかりでスパースと言えます。
スパースという特徴を用いて、信号が僅かにしかないピクセル(全ピクセルの75%)を0に置換した画像ですが、十分に綺麗な写真ではないでしょうか?(厳密には圧縮によるデータ欠損がありますが、Lenaの美貌は損なわれていないでしょう・・)
なぜ十分に綺麗なのかと言いますと、ウェーブレット圧縮はMRIにおいて大切な輪郭情報とコントラスト情報を上手く保存しやすい圧縮技術だからです。
そこで、圧縮センシングMRIの発想は、圧縮画像でも情報が担保されているならば、最初から圧縮画像を目標に再構成しようとするものです。
【圧縮センシングMRIの概略】
次に圧縮センシングMRIの概略図を示します。図のスパース画像(ウェーブレット画像)において“L1ノルムの最小化” という言葉が現れます。L1ノルムという言葉が難しいかもしれませんが、ただ単純に全ピクセルの絶対値の合計です。
このL1ノルムを最小化していく作業が、前述したスパースという特徴を用いてウェーブレット圧縮することに相当します。
ただし、どこまでL1ノルムを最小化(画像圧縮)してもよいのでしょうか?L1ノルムを小さくしすぎると画像を圧縮しすぎてしまい、データ欠損をおこして画質の劣化してしまうことが想像できます。裏を返せば、丁度いい圧縮の程度があるということです。
そのときに大事なポイントが上の概略図に示すように、“算出したk-space”が“観測したk-space”と比較して、あまりかけ離れないように制限をかけることです。具体的には、“算出したk-space”と“観測したk-space”の差の二乗和を算出して、この値が一定以上に大きくならないように設定することです。そうすれば、丁度いい圧縮の程度にL1ノルムは最小化します。つまり、
①観測したk-spaceとの整合性を保ちながら
②スパース空間にてL1ノルムの最小化する
ことが圧縮センシングMRIのカラクリになります。
【圧縮センシングMRIの数学】
ここで、もう少し、数学的な話に発展します。
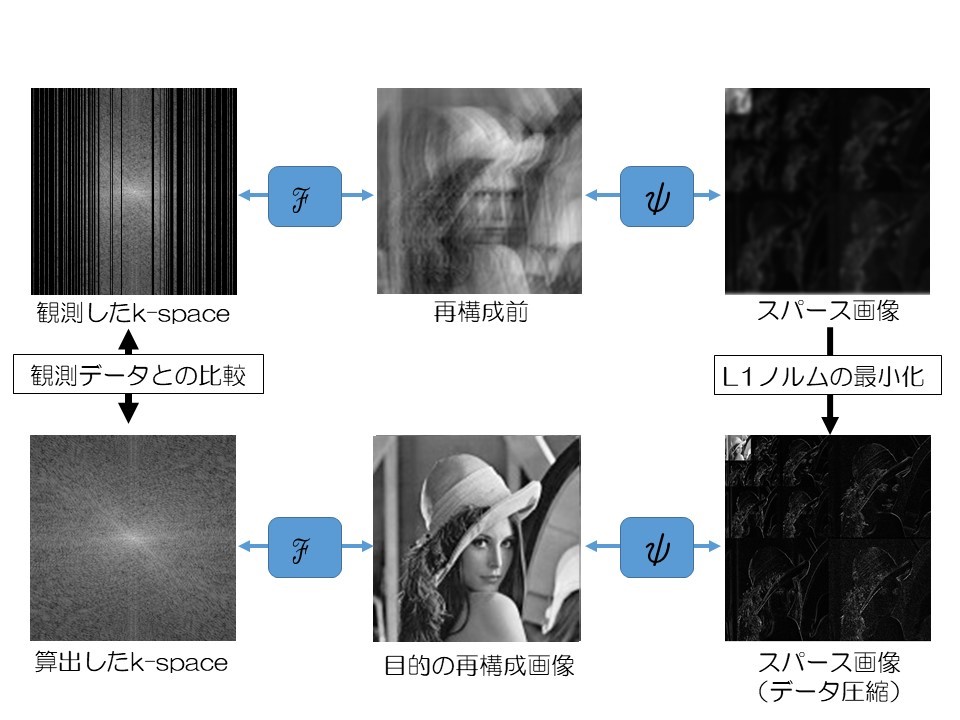
先ほどの圧縮センシングの概略図に変数や定数、演算子などの文字を用いて、新たに表現します。
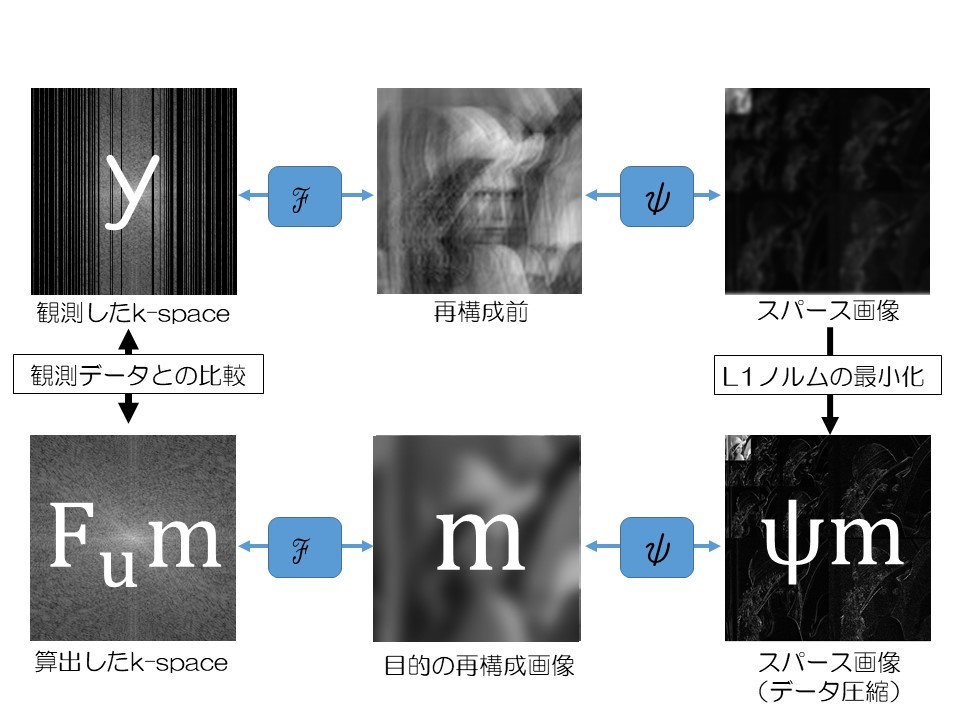 ここまで説明してきた圧縮センシングの概略を上の図で示した文字を用いて数式で表すと、下記の式となります。
ここまで説明してきた圧縮センシングの概略を上の図で示した文字を用いて数式で表すと、下記の式となります。
Fu:フーリエ変換演算子(&アンダーサンプリング)
m: 目的のMR画像データ(圧縮センシングによる画像再構成データ)
y: 観測したk-spaceデータ(高速撮像のためにアンダーサンプリングされたデータ)
λ: L1ノルム正則化係数
Ψ: スパース変換演算子(ウェーブレット変換など)
この式が①観測したk-spaceとの整合性を保ちながら、②スパース空間にてL1ノルムの最小化するということを示しています。
その意味を紐解いていきます。上式は、2つの項で構成されています①と②です。この和が小さくなるようなmを求めなさいというアルゴリズムです。
まず①という式ですが、L2ノルムという見慣れない形をしていますが、簡単にいいますと、算出したk-space“”と観測したk-space“y”の全ピクセルの差の二乗和です。つまり、先ほど概略で説明したことです。
つまり、が小さくなるということは、①観測したk-spaceとの整合性を保つという意味を持ちます。
次に②という式ですが、これはスパース画像のL1ノルムを示します。繰り返しになりますが、ただのスパース画像における全ピクセルの絶対値の合計です。
つまり②が小さくなるということは、②スパース空間にてL1ノルムの最小化するという意味を持ちます。
この2つの意味をもった項を足したアルゴリズムを最小化する問題を解くことが、①観測したk-spaceとの整合性を保ちながら、②スパース空間にてL1ノルムの最小化するを表します。
実際にこのアルゴリズムが最も小さい値をとなるようなmを求めることが圧縮センシングMRI画像を再構成するということになります。
つまり、この式が圧縮センシングの画像再構成の全てであり、圧縮センシングの特徴を示すと考えます。
したがって、m以外の変数によって、目的のMR画像データの特徴がつけられると考えられます。
【L1ノルム正則化係数】
圧縮センシングMRIの数学において、特に解釈の難しい変数がλ(L1ノルム正則化係数)であると言えます。この変数λはMRの観測データや撮像パラメータに関するものではなく、上式の最適化問題を解くためのただの定数に過ぎません。したがって、λは任意に設定して解くことになります。つまり、λの設定次第では様々な解が存在することになり、いろいろな再構成画像が生まれるということになります。臨床機においてλの設定がどのようにできるかどうかはわかりませんが、経験的な設定が必要であることが考えられます。
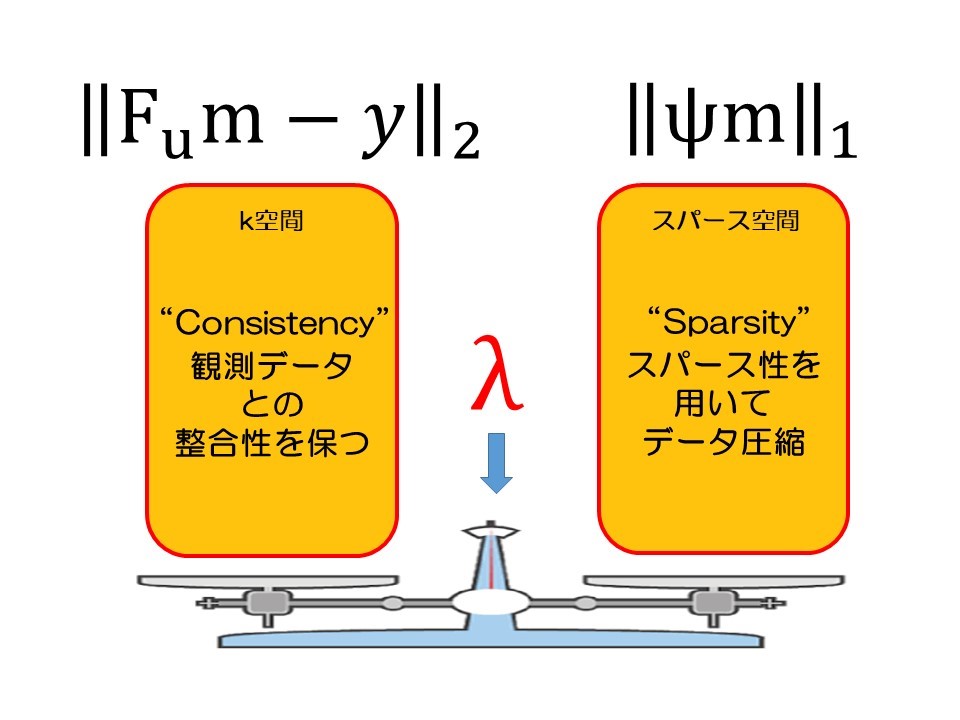
ここで、λの簡単な概念を図に示します。
先ほどから示している式は2つの項に分かれており、λは2つの項のバランスをチューニングしています。式の左側は観測データとの整合性、右側はスパース性を用いたデータ圧縮の程度を表します。そしてλの解釈が難しいのは観測データとの整合性を保つということと、画像圧縮するということとは相反する操作であるからです。
例えばλにゼロを設定すると、観測したアンダーサンプリングデータに忠実な画像再構成結果を得ることになります。つまり、圧縮センシングの恩恵が得られず、数式的には観測データとの最小二乗フィッテイングをしていることとあまり変わりません。恐らく、アンダーサンプリングすることで生じるノイズ様アーチファクトが残ったままの画像が再構成されることになります。
またλを極端に大きくすると左側の影響が弱いため、画像圧縮が強くなりすぎ、元画像とかけ離れた画像再構成になる可能性があります。
したがってλを上手く設定することで、アンダーサンプリングによるノイズ様のアーチファクトを除去した最適な画像再構成ができると考えられます。
【最後に】
ここで紹介したアルゴリズムはラグランジュ関数といい、最適化問題に多用される定番の式です。そして、どうして “L1ノルムの最小化”という方法で、丁度いい圧縮程度に落ち着くかというと、“最適化問題の数学”をもう少し詳しく説明しなければなりません。本当は説明したいところですが、一先ず、ここでは割愛します。機械学習やDeep Learningでも必ず登場する数学概念なので、私自身もう少し理解を深める必要があると考えております。
【自己紹介】
以前Radっていいともでも登場した、上山毅(うえやまつよし)と申します。京都出身で大阪大学から大阪大学大学院と進み、大阪府にあります彩都友紘会(さいとゆうこうかい)病院に勤め、現在は東京大学医学部附属病院で放射線技師として勤務しております。
コメント
トラックバックは利用できません。
コメント (0)

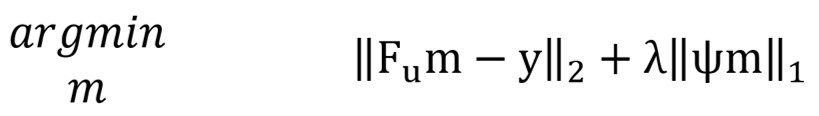






















この記事へのコメントはありません。